Selective Reflections for the Nelder-Mead Algorithm

Background

The Nelder-Mead algorithm is used to find the smallest value of a function. The algorithm first evaluates the function at a set of points, called the simplex. Then the algorithm replaces the worst point with a new point generated via a geometric reflection of the worst point through the simplex. The most basic movement is called a reflection.

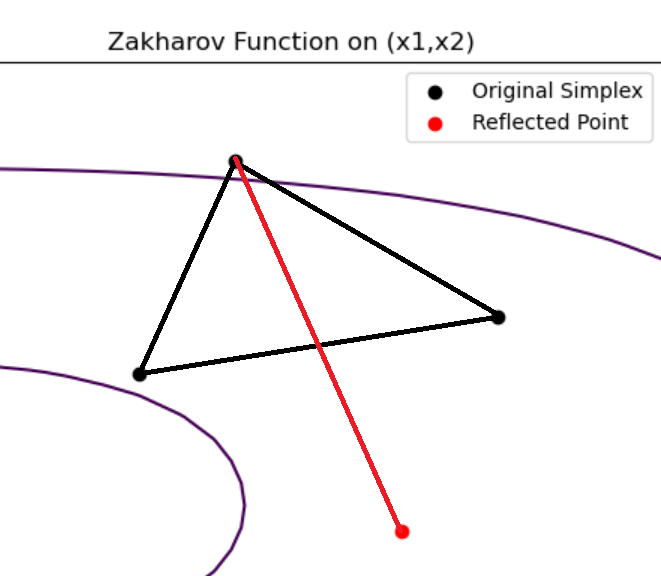
Here a basic reflection is showed on a two-dimensional simplex. The example function is the Zhakarov function in two dimensions. The result is like the original simplex has been flipped over onto a new side. The Nelder-Mead algorithm will evaluate this new point, and whether or not it is a large improvement, a failure, or falls in-between the evaluations of the rest of the simplex, the algorithm will either lengthen or shorten the reflection line, resulting in a differently shaped simplex. After many iterations, the simplex will shrink down onto a minimum and the algorithm will complete.

The Nelder-Mead algorithm does not use derivative information of the function, so it is often used when a function is unknown, complicated, or noisy. The goal of my project was to find an improvement to the original algorithm. This means identifying alterations to the original algorithm that make it find a more accurate minimum, with fewer function evaluations.

My Research Process

My research was split into two parts. First, I sought out an improved algorithm by employing genetic programming. Genetic programming is used to stochastically generate solutions to problems. Then, due to the slow search time and underwhelming results I switched to a direct and manual search. In the second phase I tested changing the angle of reflection, decision-making, and geometric properties of the basic algorithm.

Phase 1: Genetic Programming

I started with genetic programming because I wanted to be able to search through a large number of possible improvements quickly, and then take the most successful improvements and fine-tune them manually. So I created a genetic algorithm (which is a specific use-case of of a genetic program). The genetic algorithm had the goal of producing new Nelder-Mead inspired algorithms to minimize functions with. My genetic algorithm began with an initial population of randomly generated algorithms. Then the programs were tested on various optimization testing functions, and given a score based on the quality of minimums they found. Then my genetic algorithm would select the better performing individuals to pass on into the next generation and use them to generate new individuals based on the parents. After enough iterations, the genetic algorithm would complete and the best individuals would be returned for me to investigate.

I made many alterations to my genetic algorithm. The alterations ranged from its overall structure, how it generated new children, how it scored individuals in the population, how often individuals were scored, and the basic building blocks of individuals in the population. Often to test a new type of reflection I would add the reflection into the building blocks of the program.

The genetic algorithm took a long time to run, often 8-12 hours on my laptop to terminate and produce a new algorithm. So with each change to the genetic algorithm, I had to re-run, look at the results, and then make new changes based off the previous results. This was a slow process. And due to the stochasticity of genetic programming, results were extremely variable even when running the genetic algorithm again with no new changes. As the summer progressed, my mentor and I decided to move onto a new approach because the results were not reaching quality of the standard Nelder-Mead algorithm and I wanted to test other ideas more directly.

Phase 2: Direct Search

During this part of my research, I manually wrote new algorithms (rather than have my genetic algorithm automatically generate them) that were based upon the original Nelder-Mead algorithm. The original reflection direction maintains the shape of the simplex (as shown in the picture above), however I tested several different reflections that incorporated more of the information stored in the simplex. The reflections used the ranking of all the points against each other to search for the minimum, they used the actual evaluations of each point in the simplex, and the mirror reflection used a different interpretation of a geometric reflection to generate the next simplex. Shown below is an example of some of the reflections.

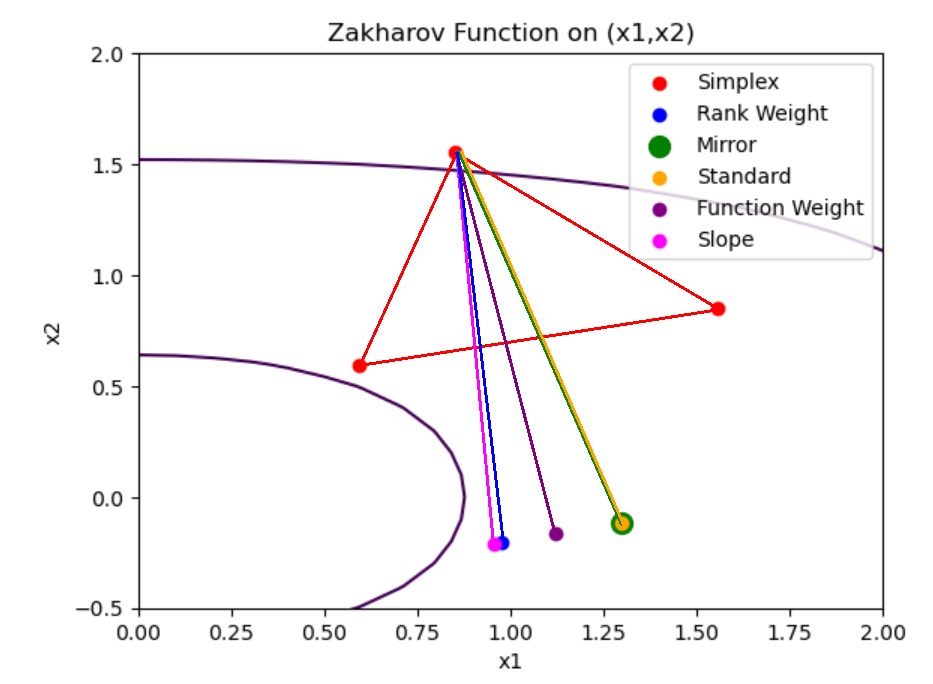
In this example, the reflections were all reasonably in the same direction, however with different simplexes, or a different test function, the reflections could be drastically different. I tested using these reflections alone, or in combination with each other.

I also tested increasing the number of points stored in the simplex. This would mean instead of using three points (forming a triangle) in two dimensions, my algorithm would use four points (forming a quadrilateral). I also tested increasing the number of points that were reflected in each iteration beyond just one.

This part of my research was quicker. Manually programming each change was just as fast (if not faster) as adjusting the genetic algorithm, and I did not need to weight half of a day to get my results. I also could directly investigate specific ideas to improve the algorithm which made the project more focused.

Results

I found that the additional point to the simplex improved the performance of the base algorithm without any changes to the reflective direction as the dimension of the function increased. The mirror transformation used with the extra point also helped the algorithm perform faster on multiple test functions, and find more accurate minimums. However, more aggressive reflections that did not uphold the shape of the simplex as closely as the standard reflection or mirror reflection would often cause the algorithm to fail to find an acceptable minimum or perform within an acceptable speed.

My most successful algorithm used an extra point in its simplex, and reflected the worst point with a mirror reflection, and the second-worst point with the standard Nelder-Mead reflection.